比の練習問題① 基礎編
比の基本問題
こちらは、比の基本問題を載せているページです。
比の詳しい解説はこちら、標準問題はこちら、応用問題はこちらへどうぞ。
(1)10:25
(2)0.2:0.6
(3)0.15:0.7
| (4) | 5 | : | 3 | |
| 6 | 8 |
(1)10:25
どちらも5で割れるので、5で割ります。
10:25=(10÷5):(25÷5)
=2:5
よって答えは
2:5
(2)0.2:0.6
小数なので、どちらも10倍します。
0.2:0.6=(0.2×10):(0.6×10)
=2:6
=1:3
よって答えは
1:3
(3)0.15:0.7
小数なので、どちらも100倍します。
0.15:0.7
=(0.15×100):(0.7×100)
=15:70
=3:14
よって答えは
3:14
| (4) | 5 | : | 3 | |
| 6 | 8 |
分数なので、分母の最小公倍数をかけます。今回は6と8の最小公倍数である24をかけます。
| 5 | : | 3 | |
| 6 | 8 |
| = | ( | 5 | ×24):( | 3 | ×24) | |||
| 6 | 8 |
=20:9
よって答えは
20:9
(1)5m:30cm
(2)0.3g:900mg
(3)0.27kL:45000mL
(4)9分:27秒
(5)1m²:300cm²
(6)63a:70ha
(7)56000m³:1km³
(8)時速90km:秒速30m
(1)5m:30cm
単位の違う比の計算は、まずは単位をそろえてから計算しましょう。(単位変換の方法はこちら)
今回は「cm」で単位をそろえます。
5m:30cm=500cm:30cm
=50:3
よって答えは
50:3
(2)0.3g:900mg
単位を「mg」でそろえます。
0.3g:900mg=300mg:900mg
=1:3
よって答えは
1:3
(3)0.27kL:45000mL
単位を「L」でそろえます。。
0.27kL:45000mL=270L:45L
=6:1
よって答えは
6:1
(4)9分:27秒
単位を「秒」でそろえます。
9分:27秒=540秒:27秒
=20:1
よって答えは
20:1
(5)1m²:300cm²
単位を「cm²」でそろえます。
1m²:300cm²
=10000cm²:300cm²
=100:3
よって答えは
100:3
(6)63a:70ha
単位を「a」でそろえます。
63a:70ha=63a:7000a
=9:1000
よって答えは
9:1000
(7)56000m³:1km³
単位を「m³」でそろえます。
56000m³:1km³
=56000m³:1000000000m³
=7:125000
よって答えは
7:125000
(8)時速90km:秒速30m
単位を「時速km」でそろえます。
時速90km:秒速30m
=時速90km:時速108km
=5:6
よって答えは
5:6
(1)5:12=a:30
(2)4:6=5:a
(3)3:a=0.16:0.3
(4)15:8=(a+3):6
(2)4:6=5:a
同じように計算をしていきますが、初めに「4:6」を簡単な整数な比に直しておくと計算が楽です。
4:6=2:3
それでは「内側のかけ算=外側のかけ算」で計算しましょう。
4:6=5:a
2:3=5:a
2×a=3×5
2×a=15
a=15÷2
a=7.5
よって答えは
a=7.5
(3)3:a=0.16:0.3
まずは、「0.16:0.3」を簡単な整数な比に直します。
0.16:0.3=16:30
=8:15
それでは「内側のかけ算=外側のかけ算」で計算しましょう。
3:a=0.16:0.3
3:a=8:15
8×a=3×15
8×a=45
a=45÷8
a=5.625
よって答えは
a=5.625
(4)15:8=(a+3):6
カッコの計算が混ざっていますが、気にせず「内側のかけ算=外側のかけ算」で計算します。
15:8=(a+3):6
8×(a+3)=15×6
8×(a+3)=90
a+3=90÷8
a+3=11.25
a=11.25-3
a=8.25
よって答えは
a=8.25
(1)A:B=3:4、B:C=3:5のとき、A:B:Cを求めましょう。
(2)A:B=2:7、A:C=0.35:0.63のとき、A:B:Cを求めましょう。
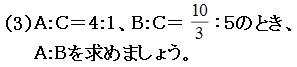
(1)A:B=3:4、B:C=3:5のとき、A:B:Cを求めましょう。
3つ以上の比を連比といいます。2組以上の比を1つの連比にまとめるときは、同じ部分を同じ数字(最小公倍数)にそろえます。
今回はどちらの比も「B」がふくまれているので、Bを「4」と「3」の最小公倍数の「12」にそろえます。
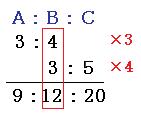
よって答えは
9:12:20
(2)A:B=2:7、A:C=0.35:0.63のとき、A:B:Cを求めましょう。
まずはA:Cの「0.35:0.63」を、簡単な整数の比に直しましょう。
0.35:0.63=35:63
=5:9
今回はどちらの比にも「A」がふくまれているので、Aを「2」と「5」の最小公倍数の「10」にそろえます。

よって答えは
10:35:18
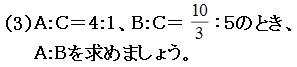
まずは、B:Cを簡単な整数な比に直します。
| 10 | :5=10:15 | ||
| 3 |
今回はどちらの比も「C」がふくまれているので、Cを「1」と「3」の最小公倍数の「3」にそろえます。

なので、「A:B=12:2」です。
12:2=6:1
よって答えは
6:1
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!