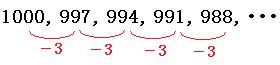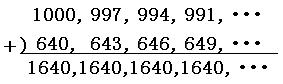数列の練習問題② 標準編
数列の標準問題
こちらは、数列の標準問題を載せているページです。
数列の詳しい解説はこちら、基本問題はこちら、応用問題はこちらへどうぞ。
2, 5, 8, 11, 14, 17, ・・・
この数列は、初めの数が2、公差が3の等差数列です。
N番目の整数は、「初めの数+公差×(N-1)」で求められるので、
2+3×(101-1)
=2+3×100
=2+300
=302
よって答えは
302
5, 12, 19, 26, 33, ・・・
(1)85番目の数はいくつでしょう。
(2)698は何番目の整数でしょう。
(3)この数列には、3けたの整数が何個並んでいるでしょう。
(1)85番目の数はいくつでしょう。
この数列は、初めの数が5、公差が7の等差数列です。
N番目の整数は、「初めの数+公差×(N-1)」で求められるので、
5+7×(85-1)
=5+7×84
=5+588
=593
よって答えは
593
(2)698は何番目の整数でしょう。
N番目の整数は、「初めの数+公差×(N-1)」で求められるので、
初めの数+公差×(N-1)=第N項
5+7×(N-1)=698
7×(N-1)=698-5
7×(N-1)=693
N-1=693÷7
N-1=99
N=99+1
N=100
(□や文字を求める計算の解き方)
よって答えは
100番目
(3)この数列には、3けたの整数が何個並んでいるでしょう。
まずは、最初の3けたの整数がいくつになるのかを求めます。3けたの整数で一番小さい数は100なので、100が第何項になるのかを求めます。
初めの数+公差×(N-1)=第N項
5+7×(N-1)=100
7×(N-1)=100-5
7×(N-1)=95
N-1=95÷7
N-1=13あまり4
つまり、(N-1)が13だと100までは届かず、(N-1)が14だと100を超えることがわかります。
よって、N=15の時に初めて3けたの整数になります。念のため、第15項がいくつになるのかを求めてみましょう。(実際に問題を解く時には求める必要はありません。)
5+7×(15-1)
=5+98
=103
ということで、初めて3けたの整数になるのは第15項です。
では、最後の3けたの整数をもとめましょう。3けたの整数で一番大きい数は999なので、先ほどと同じように999が第何項になるのかを求めていきます。
初めの数+公差×(N-1)=第N項
5+7×(N-1)=999
7×(N-1)=994
(N-1)=142
N=143
よって、最後に3けたの整数になるのは第143項です。
それでは、3けたの整数が何個並んでいるかを求めていきます。
気をつけてほしいのは、単純にひき算をしてしまうと、初めの第15項を数えていないことになってしまうということです。植木算の考え方ですね!
(植木算の解説はこちら)
143-15+1=129
よって答えは
129個
| 1 | , | 3 | , | 5 | , | 7 | , | 9 | ,・・・ | ||
| 4 | 7 | 10 | 13 |
| 1は | 1 | なので、 | ||
| 1 |
| 1 | , | 3 | , | 5 | , | 7 | , | 9 | ,・・・ | ||
| 1 | 4 | 7 | 10 | 13 |
分母と分子を別々に考えます
分子は「1, 3, 5, 7,・・・」となっているので、初めの数が1、公差が2の等差数列です。101番目の数は、
1+2×(101-1)
=1+200
=201
よって、分子は201です。
続いて分母を考えましょう。分母は「1, 4, 7, 10,・・・」となっているので、初めの数が1、公差が3の等差数列です。101番目の数は、
1+3×(101-1)
=1+300
=301
よって分母は301です。
よって答えは
201 301
1, 4, 7, 10, 13, ・・・
(1)1番目から50番目までの数をすべて加えると、その和はいくつになるでしょう。
(2)「1+4+7+10+・・・+250」はいくつでしょう。
(3)この数列に並んでいる2けたの整数をすべて加えると、その和はいくつになるでしょう。
(1)1番目から50番目までの数をすべて加えると、その和はいくつになるでしょう。
この数列は、初めの数が1、公差が3の等差数列です。
等差数列の第N項までの和は「(初めの数+最後の数)×N÷2」で求められるのですが、最後の数がわからないので、まずは最後の数を求めます。
第50項は、
1+3×(50-1)
=1+147
=148
よって、最後の数は148です。それでは、等差数列の和を求める公式に入れてみましょう。
(初めの数+最後の数)×N÷2
=(1+148)×50÷2
=149×25
=3725
よって答えは
3725
(2)「1+4+7+10+・・・+250」はいくつでしょう。
このたし算は、初めの数が1、最後の数が250の等差数列をすべて足したものになります。 なのでまずは、「250」が第何項なのかを求めていきます。この数列は、初めの数が1、公差が3の等差数列なので、
初めの数+公差×(N-1)=第N項
1+3×(N-1)=250
3×(N-1)=249
(N-1)=83
N=84
(□や文字を求める計算の解き方)
なので、最後の数250は第84項です。
それでは和を求めましょう。
(初めの数+最後の数)×N÷2
=(1+250)×84÷2
=251×42
=10542
よって答えは
10542
(3)この数列に並んでいる2けたの整数をすべて加えると、その和はいくつになるでしょう。
まずは、最後の2けたの整数を求めます。2けたの整数で一番大き数は99なので、99が第何項かを求めていきましょう。
初めの数+公差×(N-1)=第N項
1+3×(N-1)=99
3×(N-1)=98
(N-1)=32あまり2
つまり、(N-1)が32だと99までは届かず、(N-1)が33だと99を超えることがわかります。
よって、N=33の時が最後の2けたの整数になります。では、第33項の数字を求めましょう。
1+3×(33-1)
=1+96
=97
ということで、最後の3けたの整数は、第33項で「97」です。
それでは、第1項から第33項までの和を求めましょう。
(初めの数+最後の数)×N÷2
=(1+97)×33÷2
=98×33÷2
=1617
しかし、第1項から第3項までは1けたの整数なので、その分は引いておきましょう。
1617-(1+4+7)
=1605
よって答えは
1605
1000, 997, 994, 991, 988, ・・・
(1)121番目の数はいくつでしょう。
(2)1番目から121番目までの数をすべて加えると、その和はいくつになるでしょう。
(3)403は何番目の整数でしょう。
(1)121番目の数はいくつでしょう。
この数列は等差数列です。3を引くと次の項の数になります。
等差数列のN番目の数を求める公式は、初めの数に公差を(N-1)回足すから「初めの数+公差×(N-1)」でした。今回は初めの数から3を(N-1)回引くことになります。 なので、今回使う公式は、
N番目の数=初めの数-公差×(N-1)
よって、121番目の数は、
1000-3×(121-1)
=1000-3×120
=1000-360
=640
よって答えは
640
(2)1番目から121番目までの数をすべて加えると、その和はいくつになるでしょう。
等差数列の第N項までの和の公式は、数列をちょうど真ん中で切って並べ替えて考えました。
上の図のように、数がへっていく等差数列でも、「第N項までの和=(初めの数+最後の数)×N÷2」の公式は同じように使えます。
(初めの数+最後の数)×N÷2
(1000+640)×121÷2
=1640×121÷2
=99220
よって答えは
99220
(3)403は何番目の整数でしょう。
「初めの数-公差×(N-1)=N番目の数」の公式を使って、403番目の数を求めていきます。。
初めの数-公差×(N-1)=N番目の数
1000-3×(N-1)=403
3×(N-1)=1000-403
3×(N-1)=597
N-1=597÷3
N-1=199
N=199+1
N=200
(□や文字を求める計算の解き方)
よって答えは
200番目
公式はまる覚えするだけでなく、「どうしてそうなるのか。」を知っておくと、応用問題に瞬時に対応できますよ!
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!