植木算
植木算とは
植木算とは、木の本数や、木の間の距離などを求める問題です。木ではなく、紙やリングだったりすることもあります。
文章題を解く際に、数字ばかりを追って式を作るくせのある人は、あっという間にひっかかります。
文章を読んで、しっかりと頭の中で状況を描けている人にとっては簡単に感じるでしょう。
算数というよりは、ほとんど国語の問題です。
植木算の学習を通して、文章の内容を頭の中でイメージするくせをつけてもらえればと思います。
出題パターンは大きくわけて2種類です。
- まっすぐ植える
- 円形に植える
まっすぐ植える植木算の解き方
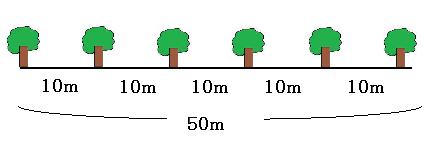
気をつけることは、木の本数と木の間の数が一致しないということです。 状況がイメージできればひっかかることはありません。イメージするのが苦手な人は、絵を描いて確かめてください。
こういう、暗算でも解けてしまいそうな数字は危険です。数字に飛びついて、ひっかからないように注意してください。状況を絵に描いてみます。
絵を見れば一目瞭然なのですが、
50m÷10m=5
の計算で出てくる「5」という数字は、木と木の間が「5個」あるという意味の「5」です。 絵を見れば、木の本数は、木と木の間の数より1つ多いので、
5+1=6
よって答えは
6本
基本的には、まっすぐに木が並んでいる場合、木の本数は、木と木の間の数よりも1つ多くなります。
円形に植える植木算の解き方
円形に木を植える問題は、中途半端に知識がある人の方がひっかかりやすいという、なんとも理不尽な問題です。
何も知らないで解いた方が間違えなかったりします。
ですが、知らないで解けても算数においては何の意味もありません!
コツは、相も変わらず「状況をしっかりイメージする」ことです。
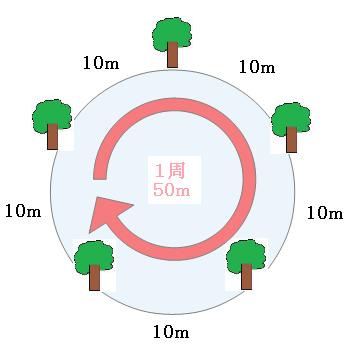
状況を絵に描いてみます。
絵を見れば一目瞭然なのですが、
50m÷10m=5
の計算で出てくる「5」という数字は、木と木の間が「5個」あるという意味の「5」です。 しかし例題1とは違って、木と木の間の数と木の本数が同じです。
よって答えは
5本
基本的には、円形に木が並んでいる場合、木の本数と、木と木の間の数は同じです。それでは植木算をまとめます。
こういったタイプのひっかけ問題はテストでもよく聞かれますし、日常生活の中にもたくさん潜んでいます。
例えば、8月10日から8月13日まで旅行に行く場合、日数は4日間になります。「え?3日間じゃないの??」って思った人は、指を使って数えてみてください。
次は、比のお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!