年齢算の練習問題②　標準編

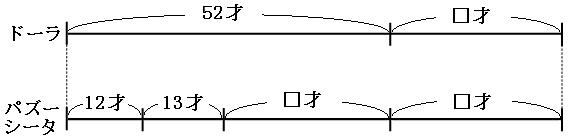
□年後に、ドーラさんの年齢が、パズーくんとシータさんの年齢の和と等しくなるとして、現在の線分図と□年前の線分図を書きます。パズーくんとシータさんの線分図は1本にまとめてしまいます。

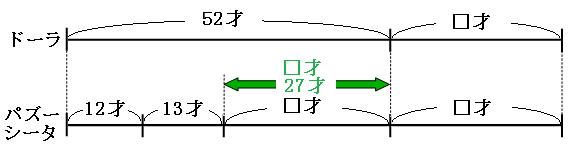
パスーくんとシータさんはどちらも□才年をとるので、パズーくんとシータさんの線分図には「□才」が2つ書かれています。また、□年後、ドーラさんの年齢と、パズーくんとシータさんの年齢の和とは等しいので、線分図の長さは等しくなっています。線分図を見比べてみましょう。

緑の矢印の部分に注目すると、

年齢
52才－（12才＋13才）＝27才

□
□2個－□1個＝□1個

□1個が27才にあたることが分かりました。もともと□年後にドーラさんの年齢が、パズーくんとシータさんの年齢の和と等しくなるという設定でした。なので答えは

27年後

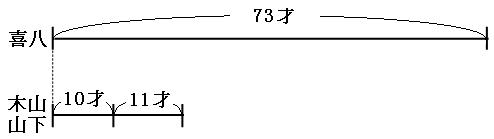
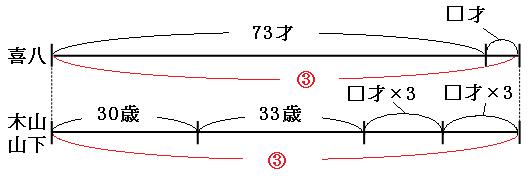
□年後に、喜八さんの年齢が、木山くんと山下くんの年齢の和の3倍になるとして、現在の線分図と□年前の線分図を書きます。木山くんと山下くんの線分図は1本にまとめてしまいます。

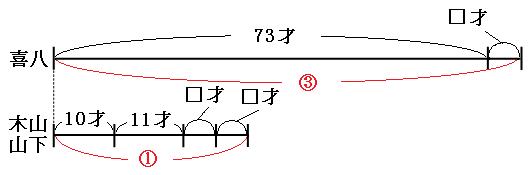
木山くんと山下くんはどちらも□才年を取るので、木山くんと山下くんの線分図には「□才」が2つ書かれています。 このままでは線分図を見比べられませんので、木山くんと山下くんの線分図を3倍に伸ばして、喜八さんの線分図と同じ長さになるようにします。線分図を3倍に伸ばすので、書いてある数字も3倍にします。

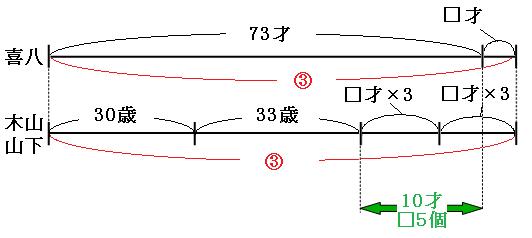
2本の線分図を見比べると、、

緑の矢印の部分に注目すると、

年齢
73才－（30才＋33才）＝10才

□
□3個＋□3個－□1個＝□5個

□5個が10才にあたることが分かりました。なので、□1個にあたる年齢は、

10才÷5個＝2才

□1個が2才にあたることが分かりました。もともと、□年後に喜八さんの年齢が、木山くんと山下くんの年齢の和の3倍になると設定していました。なので答えは

2年後

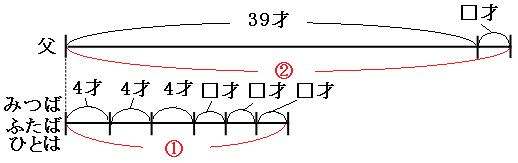
□年後に、父の年齢が、みつばさんとふたばさんとひとはさんの年齢の2倍になるとして、現在の線分図と□年前の線分図を書きます。みつばさんとふたばさんとひとはさんの線分図は1本にまとめてしまいます。

みつばさんとふたばさんとひとはさんは3人とも□才年を取るので、みつばさんとふたばさんとひとはさんの線分図には「□才」が3つ書かれています。 このままでは線分図を見比べられませんので、みつばさんとふたばさんとひとはさんの線分図を2倍に伸ばして、父の線分図と同じ長さになるようにします。線分図を2倍に伸ばすので、書いてある数字も2倍にします。

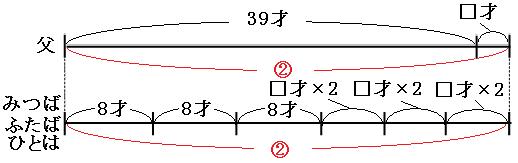
2本の線分図を見比べると、、

緑の矢印の部分に注目すると、

年齢
39才－（8才＋8才＋8才）＝15才

□
□2個＋□2個＋□2個－□1個＝□5個

□5個が15才にあたることが分かりました。なので、□1個にあたる年齢は、

15才÷5個＝3才

□1個が3才にあたることが分かりました。もともと、□年後に父の年齢が、みつばさんとふたばさんとひとはさんの年齢の2倍になると設定していました。なので答えは

3年後