売買損益の練習問題② 標準編
売買損益の標準問題
こちらは、売買損益の標準問題を載せているページです。
売買損益の詳しい解説はこちら、基本問題はこちら、応用問題はこちらへどうぞ。
割合や線分図を使います。不安な場合は復習をしておきましょう。(割合の解説はこちら)(線分図の解説はこちら)
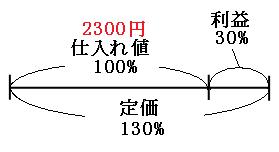
仕入れ値をもとにする量とすると、定価は「100%+30%=130%」になります。
なので定価は、
2300円×1.3=2990円
(割合の計算方法はこちら)
定価をもとにする量とすると、売り値は「100%-30%=70%」になります。
なので売り値は、
2990円×0.7=2093円
よって答えは
2093円
仕入れ値をもとにする量(100%)として、売り値を求めると、
100%×1.25×0.9=112.5%
よって、売り値は仕入れ値の112.5%にあたります。
なので仕入れ値は、
630円÷1.125=560円
よって答えは
560円
仕入れ値をもとにする量(100%)として、売り値を求めると、
100%×1.2×0.9=108%
よって、売り値は仕入れ値の108%にあたります。つまり、利益にあたる部分は8%になります。
なので仕入れ値は、
76円÷0.08=950円
20%の利益を見込んで定価をつけているので、定価は、
950円×1.2=1140円
よって答えは
1140円
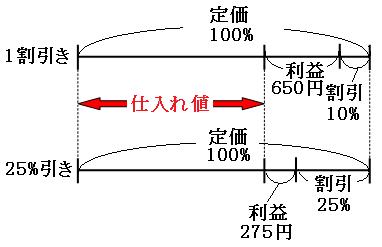
定価をもとにする量として、1割引きにしたときの線分図と、25%引きにしたときの線分図を並べて書いてみましょう。どちらも定価と仕入れ値は同じなので、定価と仕入れ値の位置を合わせて書いていきます。
それでは、この線分図を見比べてみます。
線分図の緑の矢印の部分に注目します。
割合
25%-10%=15%
お金
650円-275円=375円
これで、定価の15%が375円にあたることが分かりました。まずは定価を求めます。
375円÷0.15=2500円
仕入れ値は、どちらの線分図を使って考えても大丈夫です。今回は「1割引き」の方の線分図を使って仕入れ値を求めます。 仕入れ値は、定価から10%を割り引いて、さらに利益の650円を引いた分なので、
2500円×0.9-650円
=2250-650
=1600
よって答えは
1600円
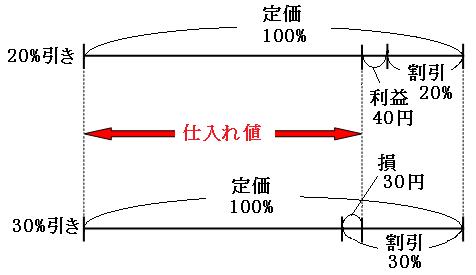
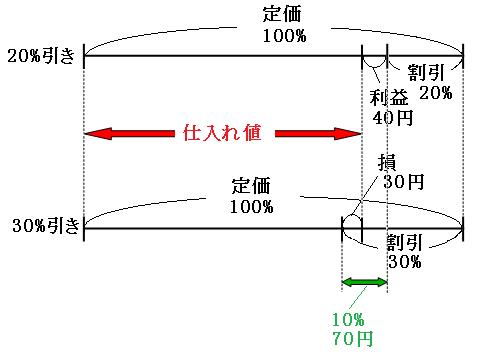
定価をもとにする量として、20%引きにしたときの線分図と、30%引きにしたときの線分図を並べて書いてみましょう。どちらも定価と仕入れ値は同じなので、定価と仕入れ値の位置を合わせて書いていきます。
それでは、この線分図を見比べてみます。
線分図の緑の矢印の部分に注目します。
割合
30%-20%=10%
お金
40円+30円=70円
これで、定価の10%が70円にあたることが分かりました。まずは定価を求めます。
70円÷0.1=700円
「20%引き」の方の線分図を使って仕入れ値を求めます。仕入れ値は、定価から20%を割り引いて、さらに利益の40円を引いた分なので、
700円×0.8-40円
=560-40
=520
よって答えは
520円
商品の定価が分からないので、自分で設定してしまいます。どんな数字で設定しても大丈夫ですが、今回は商品の定価を①円とおきます。
これを使って、商品20個を買った時の代金を求めていきます。
まずは、ディスカウントショップで買った時から考えましょう。ディスカウントショップでは10%引きで買えるので、
①円×0.9×20個=⑱円
続いて地元の商店街で買った時を考えます。15個買うと1個オマケしてもらえるので、20個買った時も1個オマケしてもらえます。よって20個買った時の代金は、
①円×19個=⑲円
品物1個あたりの売り値の比を求めるので、マジメに考えればそれぞれを20で割って、
(⑱円÷20個):(⑲円÷20個)
と、しなければならないのですが、今回は比を求めればよいので、どちらも同じ数でわり算をするのならば、はじめからわり算をする必要はありません。(あとで簡単な整数の比に直す時に、結局かけ算をして消えてしまうので)
なので、今回も20で割るのを省略しても大丈夫です。この品物1個あたりの、ディスカウントショップと地元の商店街の売り値の比は、
⑱円:⑲円
よって答えは
18:19
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!