円錐の表面積の求め方を解説。円錐の表面積の求め方は完全パターン化できる！
円錐の展開図
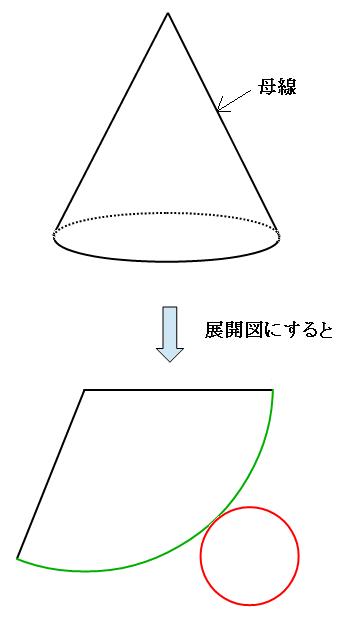
円錐の場合も、円柱と同じように展開図を書いて考えます。円錐の展開図は、底面の部分の円と、側面の部分のおうぎ形の組み合わせになります。
特に注目するのは、底面の円周（上の図の赤い部分）と、側面のおうぎ形の弧（上の図の緑の部分）は、もともと同じ所だったので、長さは同じということです。
円とおうぎ形が出てきますので、面積や弧の長さの求め方をいつでも使えるようにしておいてください。（面積の公式はこちら）
また、□や文字を使った式も使いますので、解き方を確認しておきましょう。（□や文字を求める計算の解き方）
円錐の表面積の求め方
少し手順が多いので、「苦手だな。」と思う人も多いようですが、流れとしてはワンパターンですので、一度手順を覚えてしまえば大丈夫です。
それでも難しいと感じるようならば、原因はおそらく計算練習不足にあります。分数の計算も、□や文字を求める計算もあるので、復習してからもう一度トライしてみるのも良いと思います。
（1）この円錐の側面の展開図の中心角は何度でしょう。
（2）この円錐の表面積は何cm²でしょう。
（1）この円錐の側面の展開図の中心角は何度でしょう。
まずはこの円錐の展開図を書いてみましょう。側面のおうぎ形の中心角が何度だかわからないので、適当に（カンで）書いて構いません。 90°や180°などのキッカリした角度ではなく、なるべく何でもない角度で書いた方が間違いにくいです。
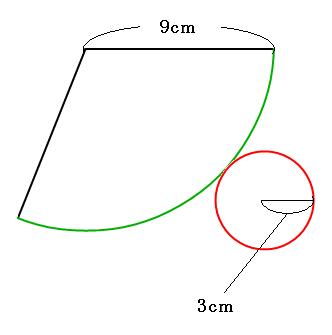
上の図の赤い部分と緑の部分の長さは同じです。赤い部分は半径3cmの円の円周なので、その長さは、
3cm×2×3.14＝18.84cm
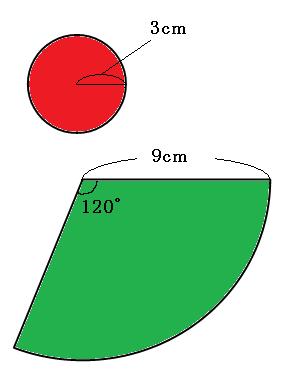
よって、緑の部分も18.84cmです。続いて、側面のおうぎ形に注目して、おうぎ形の弧の長さを求める公式を利用してみましょう。 中心角は分からないので「a」としておきます。
よって答えは
120°
（2）この円錐の表面積は何cm²でしょう。
求める面積は2つです。底面の円と、側面のおうぎ形です。
よって答えは
113.04cm²
このように、側面のおうぎ形の中心角を求めることが、円錐の表面積を求める際の一番大事なことです。
おまけとして、側面のおうぎ形の中心角と、側面の面積を一瞬で出せる裏技を書いておきます。
ただし、丸暗記は応用がきかなくなるので、「もう円錐の表面積なんて5兆回くらい求めてあきちゃったよ。」っていう人だけ覚えるようにしましょう。
側面のおうぎ形の中心角の大きさ＝底面の半径×360÷母線
側面の面積＝底面の半径×母線×円周率
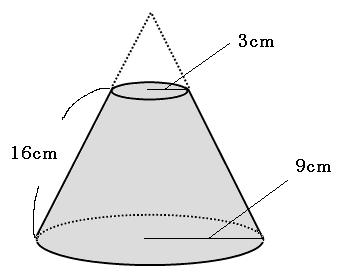
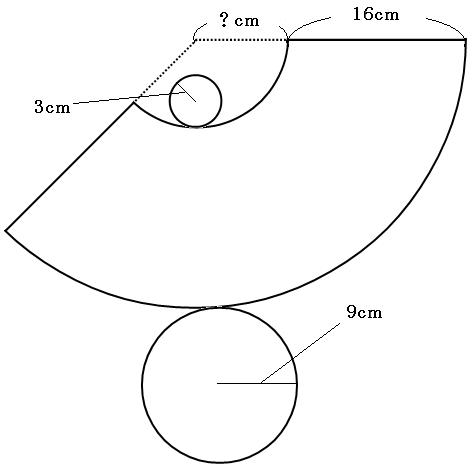
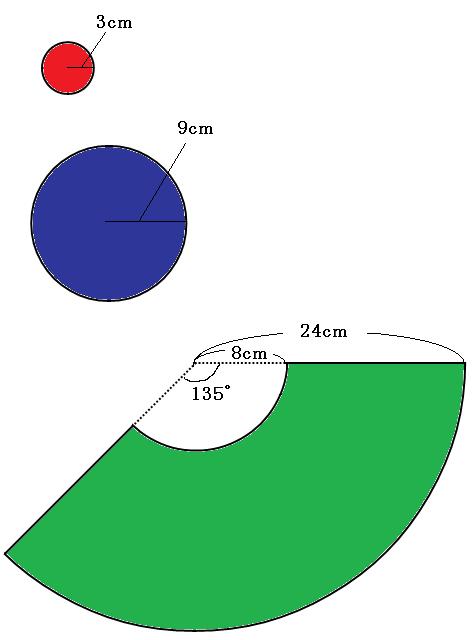
まずはこの図形の展開図を書いてみましょう。
円が2つと、おうぎ形が欠けたものが1つ出てきました。おうぎ形の部分は、全体を求めてから、いらない部分を引きましょう。
まずはおうぎ形の中心角を求めたいのですが、切り取った部分の円錐の母線の長さがわからなければ求められません。
なので、先にこの部分の長さを求めていきます。
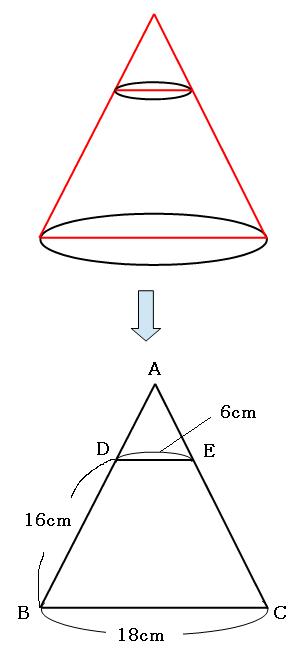
図形をよくよく見てみると、トンガリが隠れています。（相似とトンガリについてはこちら）
相似比は、
6cm:18cm＝1:3
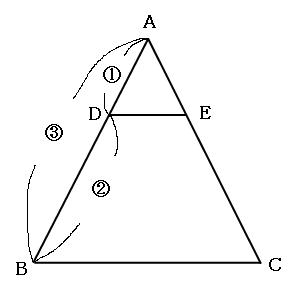
なので、AD:AB＝1:3。よって、AD:DB＝1:2
これを元にして比例式を作ると、
1:2＝□:16cm
2×□＝16
□＝8cm
（比例式の解き方）
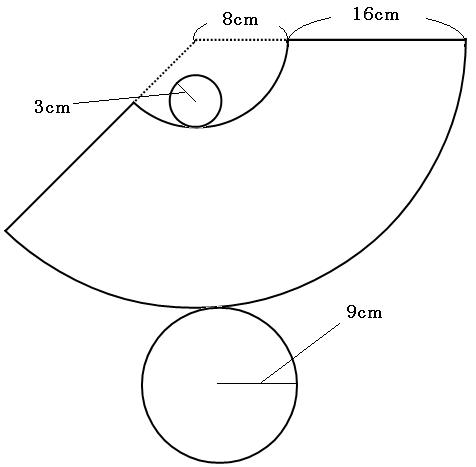
さっきの展開図に、この8cmも書き加えておきましょう。
それでは中心角を求めましょう！
赤い部分と緑の部分の長さが同じであることを利用して、おうぎ形の弧の長さを求める公式に数字を入れていきます。中心角はわからないので「a」と置きました。
中心角135°が出てしまえば、あとは面積を求めていくだけです！
上の3つの図形の面積を足せばokです。
よって答えは
885.48cm²
あれやこれやといろいろ求めましたが、やっぱりメインは側面のおうぎ形の中心角でした。
それでは、円錐の表面積をまとめます。
次は、最短距離についての問題です。
- 受験生応援オリジナルグッズ
エデュサポオリジナル受験生応援グッズ販売中！
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！
