相似比と面積比、体積比
相似比と面積比と体積比の関係
相似比とは、辺の長さの比でした。それでは面積や体積の比はどうなるのでしょうか。
相似比がa:bのとき
面積比＝（a×a）:（b×b）
体積比＝（a×a×a）:（b×b×b）
例えば長方形の面積は「たて×横」なので、たての長さも横の長さも2倍になれば「2倍×2倍」になるという理屈です。
同じように考えて、例えば直方体の体積は「たて×横×高さ」なので、たての長さも横の長さも高さも2倍になれば「2倍×2倍×2倍」になるという理屈です。
相似比から面積比と体積比を求める
では、実際にどんな計算をするのか、例題を解いてみましょう。
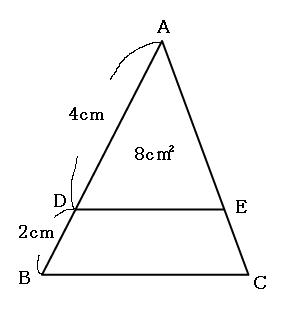
三角形ADEと三角形ABCは相似で、相似比は、
AD:AB＝4cm:6cm
＝2:3
相似比が2:3なので、三角形ADEと三角形ABCの面積比は、
（2×2）:（3×3）＝4:9
この面積比をもとにして比例式を作ると、
4:9＝8cm²:a
4×a＝72
a＝18
（比例式の解き方
求めたい台形DBCEの面積はの面積は、
三角形ABC－三角形ADE＝18cm²－8cm²
＝10cm²
よって答えは
10cm²
注意する点は2つです。トンガリの相似比を間違えないことと、比例式で出した三角形ABCの面積をそのまま答えに書いてしまわないことです。 「この計算で何が求められて、今自分は何を求めたいのか」をいつも考えながら、焦らずに解いてください。
上の図の直方体Bは、直方体Aの全ての辺の長さを2倍にしたものです。
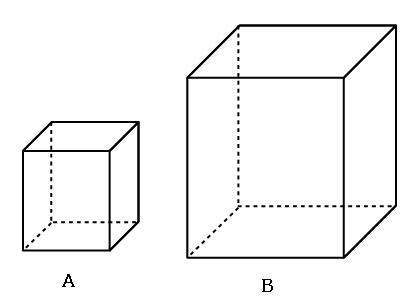
直方体Aの体積が100cm³のとき、直方体Bの体積は何cm³でしょう。直方体Aと直方体Bの辺の長さの比（相似比）は1:2です。よってふたつの直方体の体積比は、
（1×1×1）:（2×2×2）＝1:8
この体積比をもとにして比例式を作ると、
1:8＝100cm³:a
a＝800
これで、立方体Bの体積が800cm³であることがわかりました。
よって答えは
800cm³
「2を3回かけるから6だな！」というミスをやらかしやすいです。「そんなわけないじゃん。」って思うかもしれませんが、実際に問題を解いていると結構やらかします。
式をしっかり書くのが一番の予防策ですが、全ての式を書いているわけにもいかない時もあるので、何度かやらかして覚えましょう。
「あ、またやらかしてしまった！」って思った時が、一番効き目があります。
それでは、相似比と面積比、体積比をまとめます。
次は地図の話です。
