ニュートン算の練習問題①　標準編

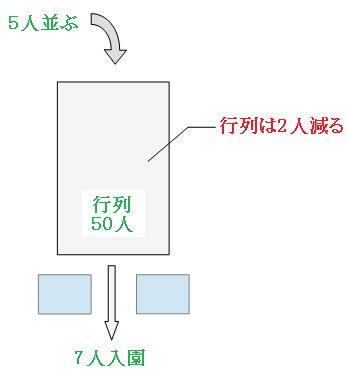
行列の最初の状況が分かっているので、1分後のことを考えましょう。
1分後、行列に5人並び、7人が入場していったので、行列の人数は2人減ったことになります。

行列の人数は1分で2人ずつ減っていくので、50人減るのにかかる時間は、

50人÷2人＝25

よって答えは

25分

行列の最初の状況が分かっているので、1分後のことを考えましょう。
360人の行列が90分でなくなったということは、1分あたりに減った行列の人数は、

360人÷90分＝4人

新たに8人並んでいるのに、行列の人数が4人減ったということは、アトラクションに乗った人数は、

8人＋4人＝12人

よって答えは

12人

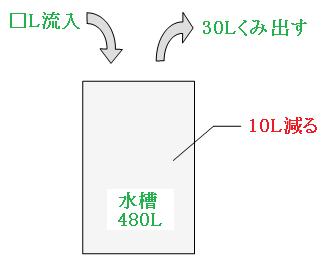
行列（水槽）の最初の状況が分かっているので、1分後のことを考えましょう。
480Lの水が48分でなくなったということは、1分あたりに減った水槽の水のかさは、

480L÷48分＝10L

30Lの水をくみ出したのに、水槽の水は10Lしか減っていません。なので、流入した水のかさは、

30L－10L＝20L

よって答えは

20L

行列の最初の状況が分からないので、線分図を書いて考えます。
まずは25分間でこの列に並んだ人数と、握手を終えた人数を求めます。

行列に加わった人数
2人×25分＝50人

握手を終えた人数
6人×25分＝150人

これを線分図で表すと、

上の線分図は、最初の人数から25分間で50人加わって、150人が握手を終えて、行列の人数が0人になった様子を表しています。 この線分図より、はじめに並んでいた人数は、

150人－50人＝100人

よって答えは

100人

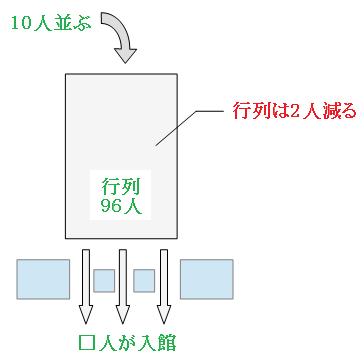
行列の最初の状況が分かっているので、1分後のことを考えましょう。
96人の行列が48分でなくなったのということは、1分あたりに減った行列の人数は、

96人÷48分＝2人

新たに10人並んだのに、行列は2人減っているということは、入館した人の人数は、

10人＋2人＝12人

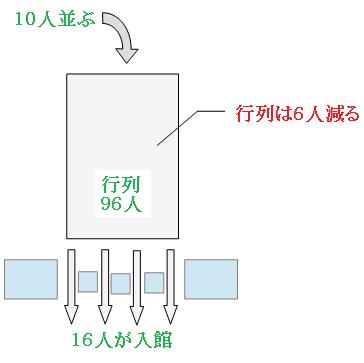
入り口が3つで12人入っていったので、1つの入口から入った人数は、

12人÷3つ＝4人

入り口を4つ開けると、1分間に入館できる人数は、

4人×4つ＝16人

新たに10人並んで、16人が入館していったので、行列から減った人数は、

16人－10人＝6人

1分間で6人ずつ行列の人数は減っていくので、96人減るのにかかる時間は、

96人÷6人＝16

よって答えは

16分