和差算の練習問題①　基礎編

和差算の基本問題

こちらは、和差算の基本問題を載せているページです。
和差算の詳しい解説はこちら、標準問題はこちらへどうぞ。
和差算は線分図を書いて、線分図の出っ張っている部分を除いて考えます。（線分図の書き方はこちら）

（基本問題1）メイさんとサツキさんがドングリを拾いました。サツキさんはメイさんより6個多く拾い、2人が拾ったドングリの個数の合計は30個でした。サツキさんは何個のドングリを拾ったでしょう。

線分図を書いて考えましょう。

出っ張っている部分を除いて考えると、

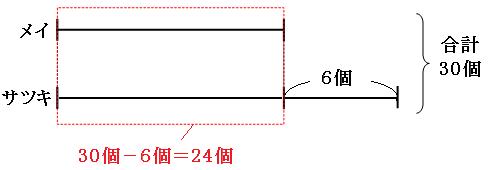
赤い四角の中の部分のドングリの個数は、

30個－6個＝24個

赤い四角の中には、同じ長さの線分が2本あるので、1本あたりは、

24個÷2＝12個

線分図を見ると、これはメイさんが拾ったドングリの個数だということがわかります。サツキさんはメイさんよりも6個多く拾っていますので、サツキさんが拾ったドングリの個数は、

12個＋6個＝18個

よって答えは

18個

（基本問題2）ココノツくんとほたるさんとサヤさんの3人でおはじきをしました。ココノツくんが取ったおはじきの数は、ほたるさんが取ったおはじきの数よりも3個多く、サヤさんが取ったおはじきの数は、ココノツくんが取ったおはじきの数よりも5個多く、3人合わせて17個のおはじきを取りました。 3人が取ったおはじきの数は、それぞれ何個ずつでしょう。

線分図を書いて考えましょう。

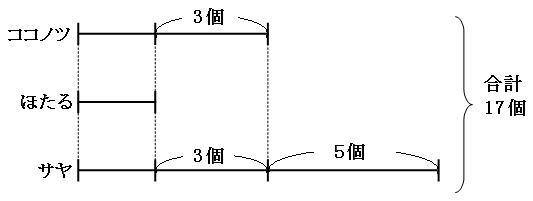
出っ張っている部分を除いて考えると、

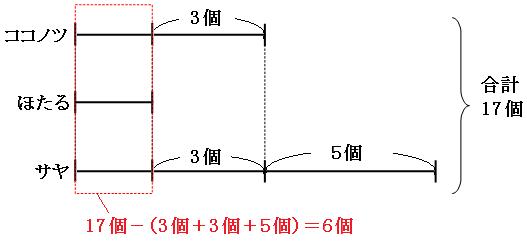
赤い四角の中の部分のおはじきの数は、

17個－（3個＋8個）＝6個

赤い四角の中には、同じ長さの線分が3本あるので、1本あたりは、

6個÷3＝2個

線分図を見ると、これはほたるさんが取ったおはじきの数だということがわかります。これを元に、それぞれが取ったおはじきの数を求めると、

ココノツ
2個＋3個＝5個

サヤ
2個＋3個＋5個＝10個

よって答えは

ココノツくん・・・5個、ほたるさん・・・2個、サヤさん・・・10個

（基本問題3）メグさん、ジョーさん、ベスさん、エイミーさんの四姉妹は、お母さんにプレゼントを買うことにしました。メグさんが買ったプレゼントはジョーさんが買ったプレゼントよりも50円高く、ペスさんが買ったプレゼントはジョーさんが買ったプレゼントより20円安く、エイミーさんが買ったプレゼントはベスさんが買ったプレゼントよりも60円高く、4人のプレゼントの代金を合計すると350円でした。メグさんが買ったプレゼントは何円でしょう。

問題文を読んでも頭がこんがらがってしまいます。ゆっくりと読みながら、線分図を書いてみましょう。

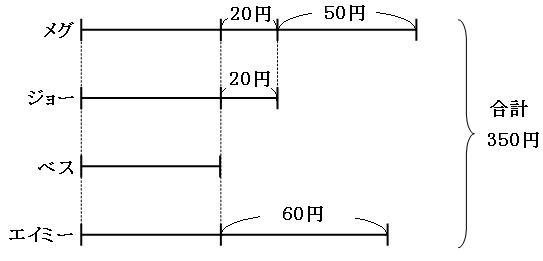
出っ張っている部分を除いて考えると、

赤い四角の中の金額は、

350円－（70円＋20円＋60円）＝200円

赤い四角の中には、同じ長さの線分が4本あるので、1本あたりは、

200円÷4＝50円

メグさんの線分図は、赤い四角の中から70円飛び出しているので、

50円＋70円＝120円

よって答えは

120円

（基本問題4）ある日の昼の長さは、夜の長さよりも3時間35分長かったそうです。昼の長さは何時間何分何秒だったでしょう。

1日の長さは24時間です。これを分に直すと、（時間の単位のかえかたはこちら）

24時間×60＝1440分

ついでに3時間35分も分に直して、

3時間×60＋35分＝215分

昼と夜の差は215分、和は1440分なので、線分図を書いてみると、

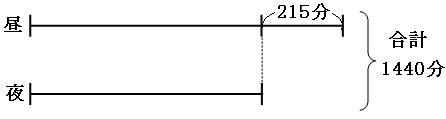
出っ張っている部分を除いて考えると、

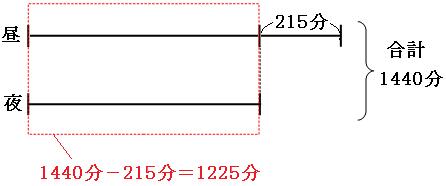
赤い四角の中の時間は、

1440分－215分＝1225分

赤い四角の中には、同じ長さの線分が2本あるので、1本あたりは、

1225分÷2＝612.5分

612分を時間に直すと、

612分÷60＝10あまり12

より、10時間12分。また、0.5分を秒に直すと、

0.5分×60＝30秒

昼の長さはこれよりも3時間35分長いので、

10時間12分30秒＋3時間35分＝13時間47分30秒

よって答えは

13時間47分30秒

和差算の練習問題① 基礎編

和差算の基本問題

関連コンテンツ

和差算の練習問題①　基礎編