速さと比の練習問題②　標準編

速さと比の標準問題

こちらは、速さと比の標準問題を載せているページです。
速さと比の詳しい解説はこちら、基本問題はこちらへどうぞ。
速さと比の問題は、「速さ」「道のり」「時間」の3つの要素の関係性をしっかりと理解する必要があります。

道のりが同じとき
速さの比＝a:bならば、時間の比＝b:a
（速さが2倍なら、かかる時間は半分）
時間が同じとき
速さの比＝a:bならば、道のりの比＝a:b
（速さが2倍で同じ時間走れば、進む道のりも2倍）
速さが同じとき
道のりの比＝a:bならば、時間の比＝a:b
（同じ速さで走っているとき、道のりが2倍になれば、かかる時間も2倍）

上記の3つの関係がまだ定着していない場合は、速さと比の基本問題で練習をしてから戻ってきてください。

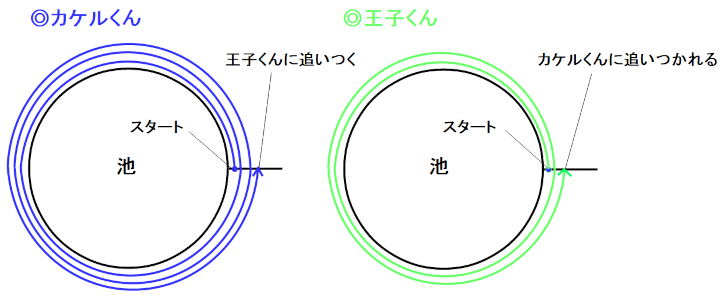
（標準問題1）カケルくんと王子くんが池の周りをランニングしています。 2人が同時に同じ方向にスタートし、王子くんがちょうど2周した所でカケルくんに追い抜かれました。カケルくんと王子くんの速さの比は、何対何でしょう。

まず気づかなければならないことは、スタートしてから王子くんがカケルくんに追い抜かれるまでに、2人が走った時間は同じであるということです(違う時間に出会うにはタイムリープの能力が必要になります)。

走った時間が同じであることをふまえた上で、今回の問題を図にしてみましょう。

カケルくんが王子くんを追い抜いたということは、カケルくんが王子くんを一周遅れにしたということです。
王子くんがちょうど2周した所でカケルくんに追い抜かれたということは、そのときカケルくんはちょうど3周したということになります。

2人が走った時間は同じなので、走った道のりの比と速さの比は同じになります。二人が走った道のりの比は、

3周:2周
＝3:2

2人が走った道のりの比が3:2ということは、速さの比も3:2ということになります。

よって答えは

3:2

（標準問題2）その日もアムロくんはいつも通りに家を出て、学校に向かって歩いていました。シャアくんは、アムロくんの机の上にあった忘れ物を届けるために、アムロくんが家を出発して10分後にアムロくんを追いかけはじめました。シャアくんの速さは、アムロくんの速さの3倍です。シャアくんがアムロくんに追いつくのは、アムロくんが家を出発してから何分後でしょう。

シャアくんの速さはアムロくんの速さの3倍なので、シャアくんとアムロくんの速さの比は3:1になります。
この事を利用して、シャアくんの速さを「分速③m」、アムロくんの速さを「分速①m」と置きます。本当に「分速3m」なわけではないので、数字は○で囲っておきます。

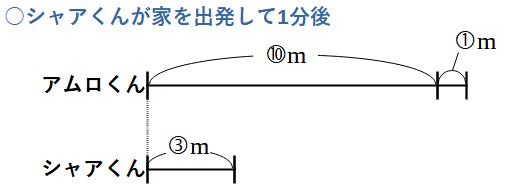
追いつく旅人算なので、シャアくんが出発した瞬間と、シャアくんが出発してから1分後と、シャアくんがアムロくんに追いついた瞬間の3つに注目します。
旅人算がわからない場合は、先に進む前に旅人算の解説を読んできてください。

シャアくんが出発するまでにアムロくんはすでに10分間歩いています。この間にアムロくんが歩いた道のりは、

分速①m×10分
＝⑩m

ということで、⑩mになります。これも、本当に「10m」なわけではないので、数字を○で囲ってあります。

次に、シャアくんが出発してから1分後のことを考えます。シャアくんとアムロくんが1分間に進む道のりは、

シャアくん
分速③m×1分
＝③m

アムロくん
分速①m×1分
＝①m

1分間でシャアくんはアムロくんに、

③m－①m
＝②m

で、②m追いつきます。
よって、⑩m追いつくために必要な時間は、

⑩m÷②m
＝5

これで、シャアくんが出発してからアムロくんに追いつくまで、5分かかることがわかりました。

求める時間はアムロくんが出発してからシャアくんが追いつくまでの時間なので、アムロくんが出発してからシャアくんが出発するまでの時間も加えて、

5分＋10分
＝15分

よって答えは

15分

（標準問題3）今日は兄弟そろって寝坊をしてしまったため、いつもより遅い午前8時5分に家を出て学校へ向かいました。兄は不良なので、いつもと同じように時速3.6kmの速さで学校に向かったところ、5分遅刻してしまいました。真面目な弟は時速9kmの速さで走って学校に向かったところ、始業時間の4分前に学校に到着しました。始業時間は、何時何分でしょう。また、家から学校までの道のりは何mでしょう。

この問題については、2つの解法パターンを解説します。どちらのパターンでも解けるようにしてください。

◎解法パターン1

時間と道のりの単位がバラバラなので、時間の単位を「分」、道のりの単位を「m」にそろえます。そのため、兄弟の速さを「分速m」にかえます。速さの単位のかえかたがわからない人は、復習をしてから戻ってきましょう。

不良兄
時速3.6km
＝時速3600m
＝分速60m

真面目弟
時速9km
＝時速9000m
＝分速150m

2人とも家から学校まで歩くので、2人が歩いた道のりは同じです。道のりが同じであれば、速さの比と時間の比は逆比になっています。［速さが早くなれば(数字が大きくなれば)、かかる時間は少ない(数字が小さい)。］

不良兄と真面目弟の速さの比は、

分速60m:分速150m
＝2:5

不良兄と真面目弟の速さの比が2:5ということは、学校につくまでにかかった時間の比は5:2ということになります。
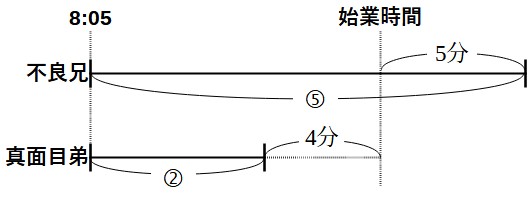
これをもとに、時間の線分図を書いてみます。

線分図が書けたら、比の数量(◯で囲ってある数字)と実際の時間が両方とも分かる区間を探します。

上の線分図の青い矢印の部分に注目します。この部分は比の数量と実際の時間が両方ともわかります。

比
⑤－②
＝③

実際の時間
5分＋4分
＝9分

したがって、③が9分に当たることがわかりました。続いて、①が何分に当たるかを求めます。

9分÷③
＝3分

これで、①が3分に当たることがわかりました。もう一度線分図を振り返ります。

不良兄の線分図に注目すると、不良兄が歩いた時間は⑤です。①が3分に当たることがわかっているので、⑤が何分になるかが求められます。

3分×⑤
＝15分

これで、不良兄は家から学校まで15分歩いたことがわかりました。午前8:05に家を出発して、5分遅刻したことを考えて学校の始業時間時間を考えます。

午前8:05＋15分－5分
＝午前8:15

これで学校の始業時間が午前8時15分であることがわかりました。
また、不良兄は分速60mで学校まで15分歩いたことから、家から学校までの道のりが求められます。

分速60m×15分
＝900m

よって答えは

始業時間…午前8時15分
家から学校までの道のり…900m

◎解法パターン2

もう一度問題を読み返してみます。

解法パターン2では、始業時間の時点での道のりに注目します。真面目弟は実際には始業時間の4分前に学校に到着しますが、そのまま立ち止まらずに4分間歩き続けると仮定します。
そのうえで、始業時間の時点で不良兄は学校まであと何mのところにいるか、真面目弟が学校より先の何mのところにいるかを考えます。

不良兄
分速60m×5分
＝300m

真面目弟
分速150m×4分
＝600m

よって、始業時間の時点で、不良兄は学校まであと300mのところにいます。真面目弟は学校の先600mのところにいます。

また、家を出てから始業時間まで、2人が歩いた時間は同じです。そのため、2人の速さの比と道のりの比は同じになります。
不良兄と真面目弟の速さの比は、先ほど2:5であると求めました。よって、不良兄と真面目弟が歩いた道のりの比も2:5となります。
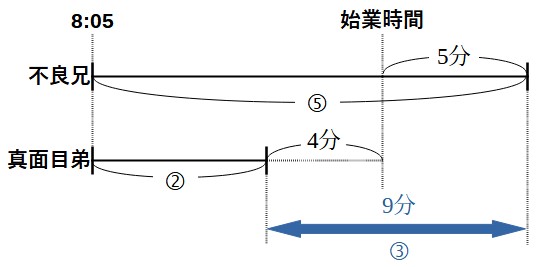
以上をふまえた上で、始業時間の状況を線分図を書いてみます。